RRRRRRRRRRRRRR. But what is R, anyways? And what's a loss factor? What does this all mean? I'll be using this blog post as a means to understand how energy from a radar signal is propagated through a medium, or more specifically, an interface between two media. As discussed in an earlier blog post, radar operates by having a sensor emit radio waves towards a target, measuring the amount of energy that is reflected back (termed the "backscatter") to gain information about physical properties of the surface, including how rough the surface is. But surfaces don't just reflect radio waves (or any kind of radiation), they can also transmit the radio wave through the medium that makes up the surface. This is the core issue behind my first project here at Western, which has to do with seeing how the radar backscatter of a surface changes if you dump a whole lot of sand on it. As you would expect, a radar wave behaves differently hitting a bare rock surface than when it hits some layer of sand atop a previously bare rock surface-- it transmits differently going from the atmosphere to a layer of sediment than going from the atmosphere to bare rock, and it also behaves differently going from a layer of sediment to rock below. This is related to the concept of the dielectric constant, which provides a sense of how well radar waves travel through certain materials. More explicitly, it's the ratio of the permittivity of the material to the permittivity of free space. You can reasonably infer that this means something like air will have a dielectric constant of 1. Pretty much all other materials have higher dielectric constants, which means radio waves will travel more slowly through them than air. For example, soil has something like a dielectric constant of 3, and rock has a dielectric constant of around 8. This means that in addition to the component of a radio wave that gets reflected from a surface, there is also a component that is transmitted through the underlying medium, and the degree of transmissivity. In a sense, part of the radio wave is lost when transmitted through a medium as opposed to being purely reflected at the surface-- and this forms the basis of something that's been troubling myself and Catherine for much of the past year.
In Campbell et al. (1997), the authors model how regolith on the lunar surface attenuates the radar backscatter. To calculate this, they have introduced several equations which involve what are called "loss factors." Essentially, these are parameters in relevant equations that detail how the radar power is lost going from one medium to another, in all cases going from a lower dielectric constant medium (like air, or the vacuum of space) to a higher dielectric constant medium. Equation 1 of Campbell et al. (1997) relates the "observed" radar backscatter of a surface to the "unmantled" radar backscatter for a surface that's been covered with lunar regolith. In addition to the radar incidence angle within the soil (given by Snell's law), there are several loss factors that modify the "unmantled" radar backscatter to produce the "observed" radar backscatter, including T, alpha, and R. T is a loss factor due to transmission effects at the regolith-space interface, while R is a loss factor due to the reduced dielectric contrast at the soil-rock boundary when compared with the rock-free space boundary. Frustratingly, in contrast to the other two loss factors, no equation is given on how to calculate R, or what the value or R should even be. Dr. Campbell has published a lot on radar and on this specific phenomena of how regolith/soil on planetary surfaces attenuates the incident radar signal, resulting in a modified radar backscatter than if the surface where just bare rock. Another paper, focusing on distinguishing volcanic regions and regolith interactions from Earth-based radar (Campbell et al., 2014) notes that the value for R is ~0.25, but again gives no equation or explanation on how to calculate R. What gives? I emailed Dr. Campbell to get more insights on what exactly the loss factor R means. His answer involves a pair of equations from his 2002 book on radar properties of planetary surfaces, which express the value for the Fresnel normal power reflectivity.
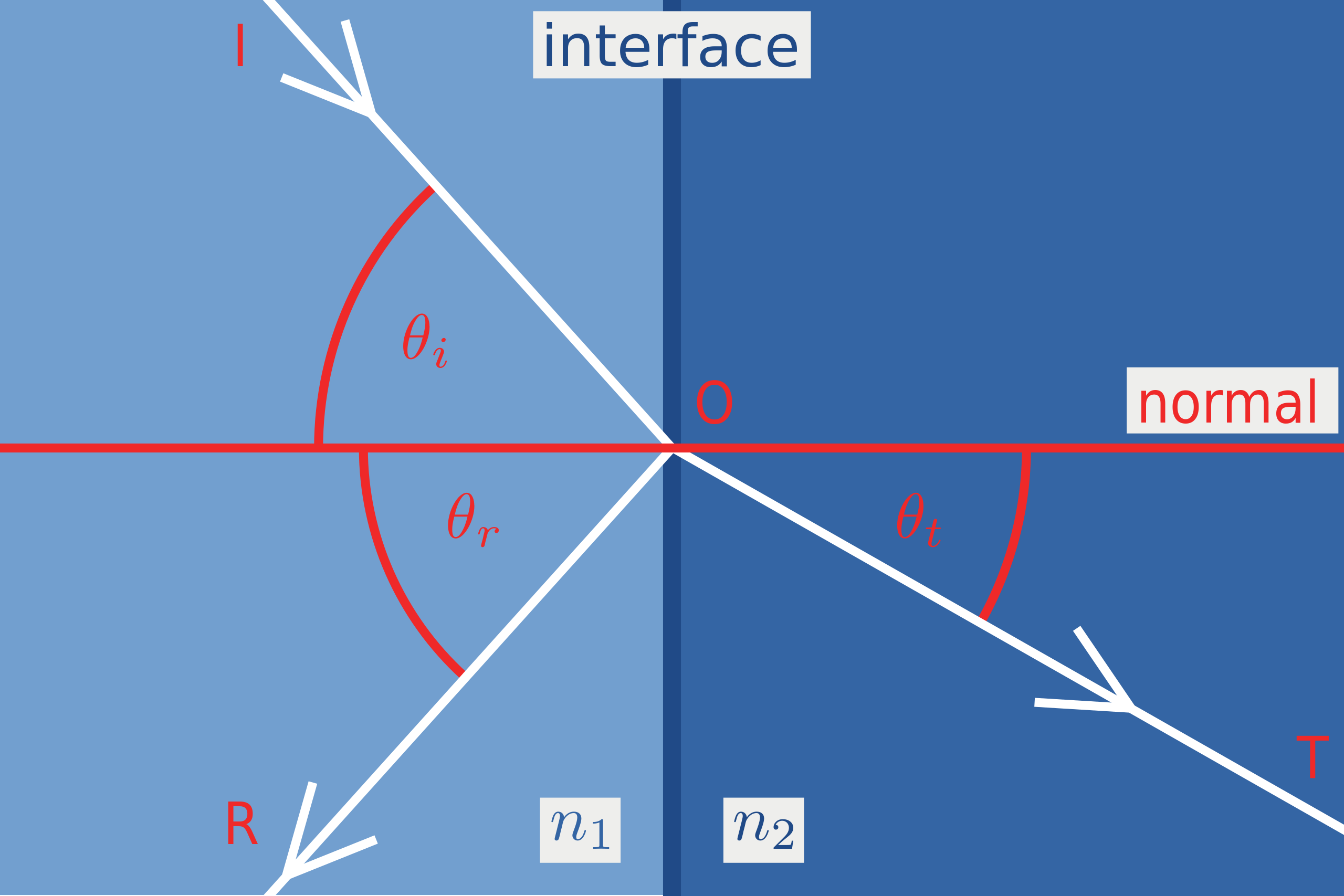
Dr. Campbell mentioned that his rationale for how to produce R was based on the fact that R is the loss factor that relates the diminished contrast between the dielectric constants between soil and rock versus rock and free space. Using modifications of the Fresnel equations, he calculated values for each pair of materials (soil-rock, soil-free space, and rock-free space). With these, he took the ratio of the soil-rock Fresnel reflectivity over the Fresnel reflectivity of that of rock-free space, and calculated the loss factor R of about 0.25. This changes our work so far by a bit, so I'll have to think about the best way to incorporate this into our current analysis. This is about all I've got, but if you'd like to talk radar loss factors, please send me an email at rperkin4@uwo.ca. Until next time!